Electrohydrodynamic jet printing
Electrohydrodynamic jet printing (EJP) is an additive manufacturing technique in which a polymeric solution or melt flowing out from the needle stretches and accelerates under the effect of an external electric field of 1 MV/m, acting between the needle and the substrate. The application of an external electric field enables the formation of a highly stable fine jet with a diameter as small as two orders of magnitude smaller than the needle diameter, as shown in figure. Consequently, micrometer resolution features can be patterned in EJP using a large-diameter nozzle due to its ability to produce geometrically independent controllable fine jet. Further, the resolution and uniformity of the printed features can be precisely controlled through proper selection of the operating parameters, such as solution flow rate, applied electric field, and stage speed. Due to its sub-micrometer printing resolution, EJP has been used for rapid prototyping of a wide range of materials successfully applied in various applications, including microlens arrays, sensors, footpaths for electronic circuits and polymeric scaffolds for tissue engineering.
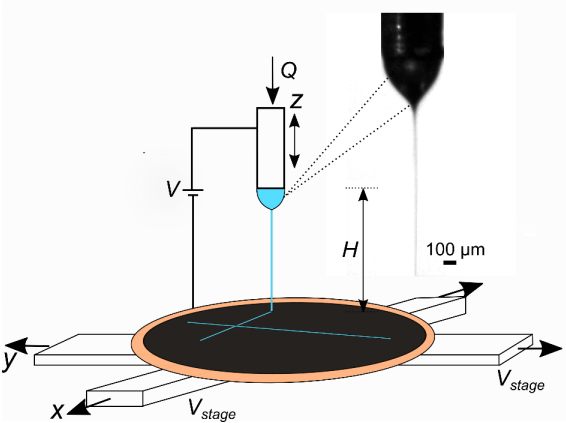 Schematic showing the EHD-jet printing setup. Also shown is a representative snapshot of the stable cone-jet. The stable cone-jet is used to deposit the polymeric ink on a substrate, which is mounted on translation stages.
Schematic showing the EHD-jet printing setup. Also shown is a representative snapshot of the stable cone-jet. The stable cone-jet is used to deposit the polymeric ink on a substrate, which is mounted on translation stages.
We have developed a fully-automated, in-house EJP setup capable of printing customized features of various polymers. We are currently working on describing the physics of the electrohydrodynamic jetting phenomenon and various applications of EJP. We have recently demonstrated the use of EJP for printing customized master molds for replica molding of PDMS microfluidic devices.
See related publication here:
pdf »
Microfluidic imaging flow cytometry
Imaging flow cytometry (IFC) is a hybrid technique that integrates microfluidic flow cytometry with optical microscopy for quantitative high-resolution digital imaging of a large number of cells. IFC has found applications in various fields, including personalized medicine, clinical diagnosis assessment, and cell phenotype profiling. The integration of microscopy with a flow cytometer has several advantages compared with the single-point detection method. Firstly, imaging allows the characterization of cell morphology, which is vital in evaluating and diagnosing numerous diseases. Moreover, unlike traditional flow cytometers, microfluidic IFC involves minimal sample and reagent consumption, lesser unit cost, and minimal contamination by using disposable microfluidic devices.
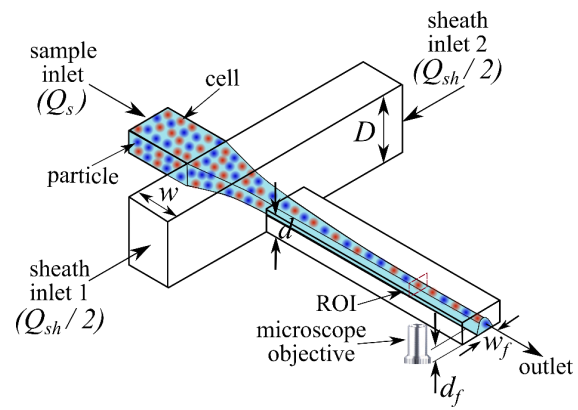 Schematic of the microfluidic chip for IFC. A mixture of cells and particles are three-dimensional hydrodynamically focused close to the bottom wall downstream of the cross-junction as the height of the sheath channel is higher than the height of the sample channel that connects the sample inlet and outlet.
Schematic of the microfluidic chip for IFC. A mixture of cells and particles are three-dimensional hydrodynamically focused close to the bottom wall downstream of the cross-junction as the height of the sheath channel is higher than the height of the sample channel that connects the sample inlet and outlet.
We are working on the development of a microfluidic imaging flow cytometer using three-dimensional (3D) hydrodynamic focusing to visualize and classify morphologically similar cells and particles from a mixture. In particular, our approach is based on the coupling of 3D hydrodynamic focusing with digital holographic microscopy for label-free classification of cells. Our technique has prospective applications in several areas, including cancer diagnostics and clinical trials.
See related publication here:
pdf »
Electrospray thrusters
Small spacecraft such as micro and nano satellites have opened up exciting opportunities to make space exploration accessible to academic and research institutions due to their low cost. However, the functionality of these spacecraft is limited due to the lack of a miniaturized propulsion system for manoeuvring and orbit control. Electrospray thrusters have emerged as a promising technology for propulsion of small spacecraft. This is due to the ability of electrospray thrusters to continuously generate nano-newton to micro-newton thrust with high specific impulse over extended period of time.
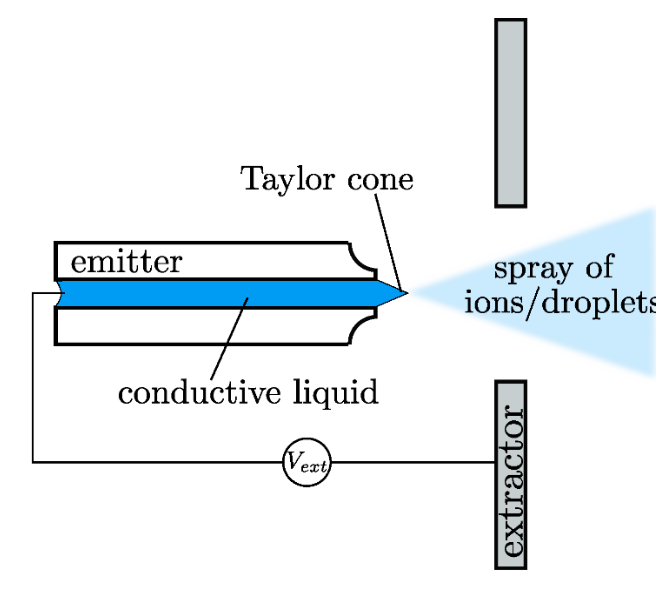 Schematic illustrating an electrospray thruster. When high voltage is applied across the conductive liquid propellant and the extractor electrode, the liquid meniscus at the tip of emitter capillary deforms into a Taylor cone and emits a spray of ions and droplets, which provides the thrust.
Schematic illustrating an electrospray thruster. When high voltage is applied across the conductive liquid propellant and the extractor electrode, the liquid meniscus at the tip of emitter capillary deforms into a Taylor cone and emits a spray of ions and droplets, which provides the thrust.
A typical electrospray thruster consists of an emitter capillary through which a conductive liquid propellant flows. A large voltage difference is applied between the conductive liquid and an annular extractor electrode. Above a threshold voltage, the liquid meniscus at the tip of the capillary deforms into a Taylor cone. At the tip of the cone, if the local electric field is on the order of 1 V/nm, it is sufficient to initiate emission of ions and droplets. The resulting electrospray provides the desired thrust, which is on the order of 10 nN for a single capillary. We are currently working on development of an in-house, high-fidelity numerical simulator for electrospray thrusters, that will be helpful in minimizing expensive and time-consuming microfabrication and testing of the thrusters during the design phase.
Deterministic lateral displacement
Deterministic lateral displacement (DLD) is a passive, size-based, label-free cell/particle separation method widely used in cell biology, biochemistry, and drug discovery. DLD utilizes specific arrangements of micro-post geometry to separate particles larger or smaller than a critical diameter. While negotiating a post, if the center of the particle diameter is larger than the critical diameter, it gets displaced laterally. On the other hand, particles smaller than the critical diameter remain centered within its initial flow stream and flow in a zigzag pattern. The critical diameter of the DLD device depends on the shape of the posts, the gap between the posts, and the angle at which the pattern of posts is tilted (also termed as the row shift factor). We are currently working on the design, fabrication, and testing of low-cost DLD microfluidic devices for biological applications, with enhanced accuracy and efficiency of separation.
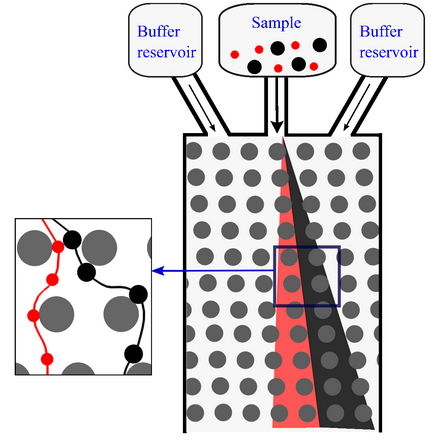 Schematic illustrating working of a DLD device. The red particles flow in a zig-zag mode because their diameter is smaller than the critical diameter. On the other hand, the black particles are displaced laterally because their diameter is larger than the critical diameter.
Schematic illustrating working of a DLD device. The red particles flow in a zig-zag mode because their diameter is smaller than the critical diameter. On the other hand, the black particles are displaced laterally because their diameter is larger than the critical diameter.
Electrohydrodynamic Instabilities in Microchannel Flows
Electrophoretic techniques such as capillary zone electrophoresis, piezoelectric focusing (IEF), and
field amplified sample stacking (FASS) are widely used as analytical tools in a variety of fields, including molecular biology, food analysis, and environmental monitoring. All electrophoretic techniques rely upon
differential migration velocities of ionic species in electrolyte solutions, under applied electric field, to
segregate constituent species of a complex mixture into distinct zones. Electrophoretic processes often involve conductivity gradients due to mismatch in sample and background electrolyte conductivity. In certain electrophoretic techniques such as FASS conductivity gradient is intentionally generated to enable sample stacking due to non-uniform electric field.
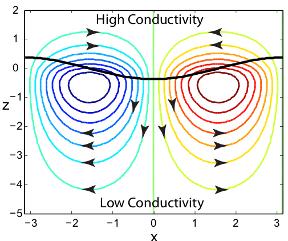 Streamlines obtained by linear stability analysis showing destabilizing electrohydrodynamic (EHD) flow in a system with colinear conductivity gradient and electric field. In this problem, an upward pointing electric field is applied externally. Charge accumulated at the interface separating high- and low-conductivity zones due to non-uniform electric field in turn couples with electric field to apply a destabilizing electric body force on the fluid.
Streamlines obtained by linear stability analysis showing destabilizing electrohydrodynamic (EHD) flow in a system with colinear conductivity gradient and electric field. In this problem, an upward pointing electric field is applied externally. Charge accumulated at the interface separating high- and low-conductivity zones due to non-uniform electric field in turn couples with electric field to apply a destabilizing electric body force on the fluid.
Presence of conductivity gradients along with high-electric field often lead to
undesirable phenomena of electrohydrodynamic (EHD) instabilities. Such instabilities result from the
coupling of electric field and fluid motion in the regions with strong conductivity gradients. Non-uniformity in electric field associated with a gradient in conductivity leads to accumulation of bulk
charge in the electrolyte solution. This bulk charge in the solution in turn couples with the local electric
field to apply a destabilizing electric body force on the fluid. Rapid mixing induced by EHD instabilities can significantly deteriorate the performance of electrophoretic processes, particularly in microfluidic devices where shorter dimensions allow higher electric fields. Therefore, investigation of EHD instabilities
and devising methodologies to inhibit such undesirable phenomenon is of paramount interest.
Contrary to their detrimental effects on electrophoretic separations, EHD instabilities can be useful for active mixing of multiple fluid streams with different conductivity in microfluidic systems. In designing such
micromixers, it is preferred that the onset of EHD instability occurs at lower electric fields. We are using
theoretical and experimental methods to come up with guidelines for optimal operational parameters to inhibit EHD flows in microscale electrophoresis, and to promote EHD instabilities in micromixers.
High-Fidelity Simulations of Microscale Electrokinetic Flows
Electrokinetic transport phenomenon deals with motion of ions and fluids under electric field, and
involves complex interaction of electrical, chemical, and hydrodynamic effects. The
nonlinearities associated with these coupled physicochemical processes pose significant challenges
in understanding the underlying physics of observed phenomena. However, the complexity of
nonlinear electrokinetic transport phenomenon also provides diverse possibilities for separation,
preconcentration, and detection of ionic species in miniaturized microfluidic devices. Example
applications of microscale electrokinetic transport include, separation of nucleic acids and proteins
from biological samples, detection of trace amounts of pollutants and toxins in environment, and
determination of additives and contaminants in foodstuffs.
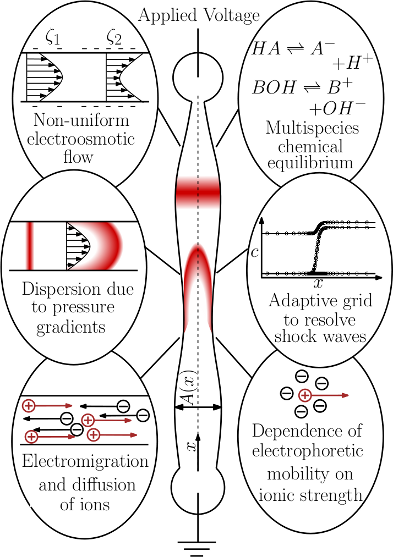 Schematic showing various physical features that should be included in a high-fidelity electrokinetics
simulation tool. Our simulation tool will enable numerical solutions of multi-dimensional electromigration-diffusion equations for non-linear electrophoresis problems in arbitrary channel geometries. The code will
use an adaptive grid refinement scheme to ensure accurate and non-oscillatory solutions while using lesser
grid points. The simulation code would also include physical modules for calculation of multispecies chemical equilibrium, and correction of electrophoretic mobilities and acid-base equilibria for finite ionic strength.
Schematic showing various physical features that should be included in a high-fidelity electrokinetics
simulation tool. Our simulation tool will enable numerical solutions of multi-dimensional electromigration-diffusion equations for non-linear electrophoresis problems in arbitrary channel geometries. The code will
use an adaptive grid refinement scheme to ensure accurate and non-oscillatory solutions while using lesser
grid points. The simulation code would also include physical modules for calculation of multispecies chemical equilibrium, and correction of electrophoretic mobilities and acid-base equilibria for finite ionic strength.
Numerical simulations offer an invaluable tool for understanding and optimizing non-linear
electrokinetic flows in complex microfluidic devices. Despite the progress in electrokinetics
simulations over past three decades, majority of computational studies are limited to one-
dimensional problems, wherein electrokinetic and hydrodynamic effects are often decoupled.
We are working towards extending the existing state-of-the-art of electrokinetic simulations by
developing an in-house, three-dimensional numerical solver for coupled species electromigration-diffusion-
reaction and Navier-Stokes equations. We will use this simulation tool to investigate nonlinear dynamics of microscale electrokinetic ion-transport in problems where multi-dimensional effects are important, including electrokinetic instabilities and shape optimization of microfluidics devices.
Uncertainty Quantification in Modeling and Simulations
Comparison of experimental data with modeling predictions is essential for making
quantitative measurements of physical properties, for example, diffusion coefficients and
species concentrations in a microfluidic T-sensor. In practice, model parameters are not known exactly due to experimental measurement
uncertainty or inherent variabilities. Therefore, deterministic models are unable to quantify uncertainty in the model predictions due to uncertainty in model parameters. Therefore, to make proper comparison between experimental data and modeling predictions, it is necessary to account for uncertainty in modeling and simulation results due to uncertainty in model parameters.
The uncertainty in model parameters which is associated with measurement errors or inherent variability in experiments can be accounted for using stochastic uncertainty quantification techniques. In particular, we employ a non-intrusive stochastic uncertainty propagation
approach based on Polynomial Chaos (PC) expansions. Unlike deterministic simulations, in this method the model parameters are treated as uncertain. For each uncertain parameter a new stochastic dimension is used to describe its probability density function. PC expansions are used to describe the dependence of model predictions on these stochastic dimensions. The coefficients or the spectral mode strengths of the PC expansions are then evaluated using numerical quadrature through multiple solutions of the deterministic model. Such an approach readily provides the uncertainty propagation information in terms of PC expansions of model predictions. Knowing the PC expansions of model predictions, the spatial variation of uncertainty and the individual contribution of each uncertain parameter to the overall uncertainty can be computed. We note that uncertainty propagation analysis can also be performed through Monte Carlo (MC) simulations, albeit with unacceptably large number of simulations. Moreover, unlike PC expansion based methods, MC simulations do not provide the coupled contribution of uncertainty in model parameters to the overall uncertainty in model predictions.
We are currently working on stochastic uncertainty quantification methods employing polynomial chaos
expansions for quantifying uncertianty in a variety of simulations due to uncertainty in model parameters.
For example, recently, we have presented an analysis of uncertainty induced in model predictions of a T-sensor based
competitive diffusion immunoassay due to uncertainty in diffusion constants, binding reaction rate constants, and inlet flow speed.
Our simulations show that the uncertainties in model parameters lead to significant spatially varying uncertainty in predicted concentration. In particular, the diffusivity of fluorescently labeled probe antigen dominates the overall uncertainty. The predicted uncertainty in fluorescence intensity is minimum near the centerline of T-sensor and relatively high in the regions with gradients in fluorescence intensity. We show that using centerline fluorescence intensity instead of first derivative of fluorescence intensity as the system response
for measuring sample antigen concentration in T-sensor based competitive diffusion immunoassay leads to lower uncertainty and higher detection sensitivity.
See related publication here:
pdf »
Previous Research Projects
Oscillating Electrolytes
The motion of ions in an electrolyte solution induced by an applied electric field is termed electrophoretic transport.
Electrophoretic transport is widely employed in analytical chemistry techniques such as capillary zone electrophoresis, isotachophoresis, and field amplified sample stacking, wherein differential electromigration velocities of ions are used for separation and in
some cases preconcentration of ionic species from sample mixtures. The differential electrophoretic velocities of ions lead to
a variety of propagating waves in ion concentrations, which are essentially propagating disturbances in the concentration
field. Previously, electrophoretic transport phenomenon was thought to exhibit only wave propagation phenomena.
Recently an "oscillating" binary electrolyte system consisting of sebacic acid and imidazole has been discovered that becomes
unstable under the influence of electric field. For particular concentrations of sebacic acid and imidazole, small
perturbations in initially uniform concentration field amplify over time under applied electric field and result in propagating,
oscillatory modes in ion concentrations.
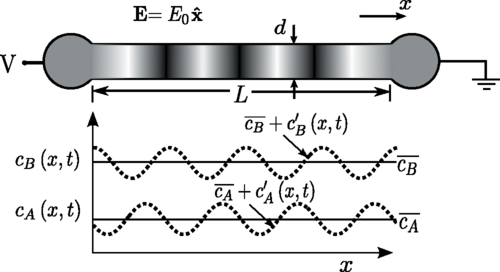 Schematic illustrating the base state and the perturbed state of an unstable electrophoretic system consisting of a binary
electrolyte. Initially, the channel is filled uniformly with binary electrolyte consisting of sebacic acid and imidazole.
When electric field is applied along the axial direction, the electrophoretic motion of ions induced in the capillary becomes
unstable and small perturbations in concentration field grow over time..
Schematic illustrating the base state and the perturbed state of an unstable electrophoretic system consisting of a binary
electrolyte. Initially, the channel is filled uniformly with binary electrolyte consisting of sebacic acid and imidazole.
When electric field is applied along the axial direction, the electrophoretic motion of ions induced in the capillary becomes
unstable and small perturbations in concentration field grow over time..
Based on linear stability analysis we have explained the physical mechanism of so-called “oscillating electrolyte” systems. We have shown that the unstable behavior is exhibited by binary electrolytes containing multivalent species having unusually high electrophoretic mobilities in higher ionization states. Presence of such multivalent species causes abnormal change in conductivity due to minor disturbances in the concentration field. The abnormal variations in conductivity then alter the local electric field in a way that further destabilizes the electrophoretic transport of ions. We note that oscillating behavior is not observed in
a majority of electrophoretic processes. However, in certain electrophoresis experiments local electrolyte composition may
be favorable to oscillations leading to spurious gradients in species concentrations.
See related publication here:
pdf »
Multi-species electrophoresis in presence of surface conduction
Electrophoresis techniques are typically characterized by linear and nonlinear concentration waves (disturbances in species
concentration) propagating under the effect of electric field. Linear concentration waves are observed in CZE where analyte concentrations are small compared with those of background electrolyte. Therefore, propagation of analyte zones in CZE does not alter the local electrical
conductivity and electric field, resulting in linear waves. For finite amplitude concentration disturbances such as those observed in ITP and during electromigration dispersion in CZE, nonlinearity in electromigration results in formation of shock and rarefaction waves.
The nonlinearity results due to the dependence of electromigration flux on local electric field, which in turn depends on the species concentrations through Ohm’s law. In CZE, nonlinear waves are undesirable as they result in unwanted dispersion of analyte zones whereas
in ITP, self-sharpening shock waves enable simultaneous preconcentration and separation of analytes between zones of high-mobility (LE) ions and low-mobility trailing electrolyte (TE) ions.
Typically electrophoresis techniques are performed in microchannels where surface conduction through the electric double layer (EDL) at channel walls is negligible compared with bulk conduction. However, when electrophoresis techniques are integrated in nanochannels, shallow
microchannels or charged porous media, surface conduction can alter bulk electrophoretic transport.
The existing mathematical models for electrophoretic transport in multi-species electrolytes do not account
for the competing effects of surface and bulk conduction.
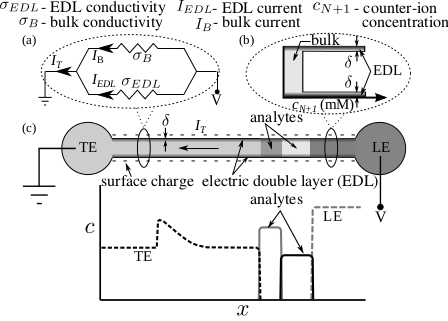 Schematic illustrating the effect of surface conduction through the EDL on bulk electrophoretic transport. We model EDL and bulk solution as resistors in parallel.
For an electrophoretic system consisting of a single counter-ionic species (having charge polarity opposite to that of
surface charge) and arbitrarily large number of co-ionic species, we model the EDL as delta distribution of counter-ions
at the channel walls with vanishingly small thickness.
Schematic illustrating the effect of surface conduction through the EDL on bulk electrophoretic transport. We model EDL and bulk solution as resistors in parallel.
For an electrophoretic system consisting of a single counter-ionic species (having charge polarity opposite to that of
surface charge) and arbitrarily large number of co-ionic species, we model the EDL as delta distribution of counter-ions
at the channel walls with vanishingly small thickness.
We have developed mathematical model of multi-species electrophoretic transport incorporating the effects of surface conduction on bulk ion-transport and provide a methodology to derive analytical solutions using the method of characteristics.
Based on the analytical solutions, we have described the propagation of nonlinear concentration waves, such as shock and rarefaction waves, and provide the necessary and sufficient conditions for their existence. Our results show that the presence of
surface conduction alters the propagation speed of nonlinear concentration waves and the composition
of various zones. Importantly, we highlight the role of surface conduction in formation of additional
shock and rarefaction waves which are otherwise not present in conventional electrophoresis. Our theory is also applicable for understanding other electrokinetic processes where surface conduction is important, including shock-electrodialysis based water deionization and concentration polarization in DC electro-osmotic pumps.
See related publication here:
pdf »
Micro heat pipes with wettability gradients
Continuous miniaturisation of electronics and increase in integration levels pose challenges in thermal management of microelectronic components. As the failure rate of microelectronic chips increases exponentially with the operating temperature, cooling of chips is essential to ensure reliable operation. Micro heat pipes (MHPs) offer an efficient means of passively removing heat from microelectronic equipment using phase change phenomenon.
A typical MHP consists of a channel with sharp edges filled with a working fluid. The sharp edges of the heat pipe allow liquid flow
due to capillary action, while the vapour flows through the inner core of channel. The figure below shows a typical triangular cross-section
MHP consisting of evaporator, adiabatic, and condenser sections. Heat input to the evaporator section vaporises the working fluid.
The local increase in vapour pressure in the evaporator section drives the vapour to relatively cooler condenser section. The
vapour condenses back to liquid in the condenser section and rejects the latent heat. The loss of liquid in the evaporator section
results in reduced radius of curvature of the liquid meniscus. Whereas, the increase of liquid in the condenser section causes
the local radius of curvature of meniscus to increase. Consequently, a pressure gradient develops in the liquid which drives the liquid
from the condenser to the evaporator section, thereby completing the cycle. Although MHPs offer a reliable and passive chip cooling
solution, MHP arrays in their current state can only transfer heat of order 10 W/sq.cm. Therefore, any further improvement in the
maximum heat transfer capacity of MHPs will help in dealing with growing challenges of thermal management of microelectronics.
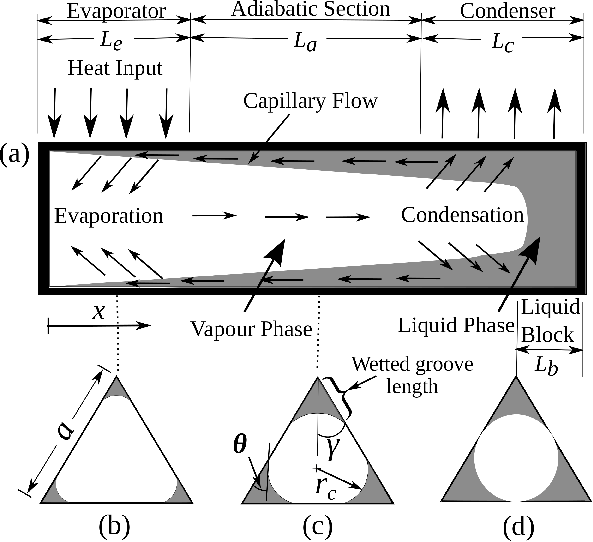 Schematic illustrating general working principle of an MHP heat pipe. Heat addition to the evaporator section vaporizes the working fluid and results in locally higher temperature and vapour pressure. Consequently, the vapour flows to the cooler condenser section where it condenses back to liquid. The condensed liquid subsequently returns to the evaporator section via capillary action through the wicks on the inner surface or due to capillary action along the sharp corners
Schematic illustrating general working principle of an MHP heat pipe. Heat addition to the evaporator section vaporizes the working fluid and results in locally higher temperature and vapour pressure. Consequently, the vapour flows to the cooler condenser section where it condenses back to liquid. The condensed liquid subsequently returns to the evaporator section via capillary action through the wicks on the inner surface or due to capillary action along the sharp corners
We have shown a new method of improving the thermal performance of MHPs by creating gradients in the wettability of
inner surface of MHPs. To quantify the effect of wettability gradients on heat transfer capacity of MHPs, we have developed a
one-dimensional mathematical model for MHP which accounts for axial variations in solid–liquid contact angle. We considered
different wettability schemes, including uniform, step-variation, and linear variation in wettability of the inner surface of MHP.
Our model predictions show that among the uniformly wetting MHPs, higher wettability surfaces show better thermal performance than the lower wetting surfaces. Interestingly, our calculations show that MHPs with higher wetting evaporator and lower wetting condenser can exhibit even better thermal performance than the MHP with corresponding uniformly higher wetting surface. We also showed that the enhancement in maximum heat transfer capacity of MHP due to wettability gradients occurs for a variety of working fluids such as water, ammonia, heptane, acetone, and methanol.
See related publication here:
pdf »
 Schematic showing the EHD-jet printing setup. Also shown is a representative snapshot of the stable cone-jet. The stable cone-jet is used to deposit the polymeric ink on a substrate, which is mounted on translation stages.
Schematic showing the EHD-jet printing setup. Also shown is a representative snapshot of the stable cone-jet. The stable cone-jet is used to deposit the polymeric ink on a substrate, which is mounted on translation stages.







